To train a tensorfow model, we call the fit() method of the model as follows:
Python
history = model.fit(X_train, y_train_one_hot,
epochs = 50,
batch_size = 32,
validation_split=0.2)The fit() method returns something called as a History object. It stores the epochwise values of the loss and any metrics we have asked the model to track.
These records can be used to visualize how the training process occurred and potentially help us modify some hyperparameters to improve the training.
We will see this with an example. We will make up one quick example, for demonstration, by generating some synthetic data.
First we will import some of the necessary packages.
Python
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow import keras
from sklearn.model_selection import train_test_split
#%% shuffle
from sklearn.utils import shuffleThe synthetic data
The synthetic data will have two classes, 0 and 1.
The training data for class 0 will be an array of numbers taken from normal distribution with mean, 2.5 and standard deviation, 0.3. Its shape will be (3000, 20), meaning that in class 0, there are 3000 samples and 20 features.
Similarly, for class 1 data, there will be 2000 samples with 20 features, from numbers taken from normal distribution with mean 2.1 and standard deviation, 0.3.
We will then concatenated the data and labels from both classes and shuffle them. Note that the labels need to be reshaped so as to be feasible with tensorflow.
Python
# x data
x_d1 = np.random.normal(2.5, 0.3, size=(3000,20))
x_d2 = np.random.normal(2.1, 0.3, size=(2000,20))
x_d = np.concatenate((x_d1, x_d2))
# y_data
y_d1 = np.zeros(3000)
y_d2 = np.ones(2000)
y_d = np.concatenate((y_d1, y_d2))
# reshape
y_d = y_d.reshape(5000,1)
# shuffle
x_d, y_d = shuffle(x_d, y_d)
print(x_d.shape)
print(y_d.shape)
print('\n First 10 labels:\n', y_d[:10])(5000, 20)
(5000, 1)
First 10 labels:
[[0.]
[0.]
[0.]
[0.]
[1.]
[0.]
[1.]
[1.]
[1.]
[0.]]We will see the distribution of values from both classes using a histogram. Here, we have to plot the arrays after flattening them, i.e. after reshaping them to one dimension.
Python
fig, ax = plt.subplots(1,1)
ax.hist(x_d1.flatten(), alpha=0.3, color='blue', label='xd_1', bins=20)
ax.hist(x_d2.flatten(), alpha=0.3, color='green', label='xd_2', bins=20)
plt.legend()
plt.show()
We see that the data from both classes come form different distribution but the range of values are still overlapping to an extent.
Training the model
We will now make the get_model function to construct the deep learning network and compile the model.
We will use accuracy and the metric to be tracked and Adam as the optimizer.
We will also use the argument learning_rate for Adam, while defining the optimizer. We can use a user defined value, lr, for the learning_rate, so that we can demonstrate the use of History object using two distinct values of lr.
Python
def get_model(lr=0.01):
# input layer
inp = keras.layers.Input(shape=x_d.shape[1:])
# dense layer
x = keras.layers.Dense(512, activation='relu')(inp)
x = keras.layers.Dense(128, activation='relu')(x)
# output layer
out = keras.layers.Dense(1, activation='sigmoid')(x)
# construct model
model = keras.Model(inputs=inp, outputs=out)
# compile model
model.compile(loss='binary_crossentropy',
optimizer = keras.optimizers.Adam(learning_rate=lr), # learning rate
metrics=['accuracy'])
print(model.summary())
return modelNow, get the model as model_1 variable with lr=0.01 and train the model.
The History object output of this training would be stored in history_1 variable.
Python
# get model
model_1 = get_model(lr=0.01)
# train
history_1 = model_1.fit(x_d, y_d,
epochs = 50,
batch_size = 32,
validation_split=0.2
)
Total params: 76,545 (299.00 KB)
Trainable params: 76,545 (299.00 KB)
Non-trainable params: 0 (0.00 B)
None
Epoch 1/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 2s 6ms/step - accuracy: 0.5807 - loss: 0.8821 - val_accuracy: 0.5700 - val_loss: 0.6411
Epoch 2/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.6223 - loss: 0.6112 - val_accuracy: 0.9870 - val_loss: 0.4832
Epoch 3/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.7103 - loss: 0.5497 - val_accuracy: 0.9480 - val_loss: 0.3893
Epoch 4/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.9554 - loss: 0.2507 - val_accuracy: 0.9970 - val_loss: 0.0641
Epoch 5/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.9925 - loss: 0.0605 - val_accuracy: 0.9970 - val_loss: 0.0298
Epoch 6/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.9346 - loss: 0.1695 - val_accuracy: 0.9950 - val_loss: 0.0765
Epoch 7/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.9907 - loss: 0.0626 - val_accuracy: 0.9980 - val_loss: 0.0235
Epoch 8/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.9971 - loss: 0.0232 - val_accuracy: 0.9930 - val_loss: 0.0338
Epoch 9/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.9918 - loss: 0.0293 - val_accuracy: 0.9950 - val_loss: 0.0391
Epoch 10/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.9284 - loss: 0.1804 - val_accuracy: 0.9960 - val_loss: 0.0320
Epoch 11/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.9970 - loss: 0.0286 - val_accuracy: 0.9880 - val_loss: 0.0536
Epoch 12/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - accuracy: 0.9873 - loss: 0.0427 - val_accuracy: 0.9970 - val_loss: 0.0135
Epoch 13/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 2s 4ms/step - accuracy: 0.9921 - loss: 0.0242 - val_accuracy: 0.9760 - val_loss: 0.0692
Epoch 14/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.9926 - loss: 0.0269 - val_accuracy: 0.9960 - val_loss: 0.0115
Epoch 15/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.9935 - loss: 0.0210 - val_accuracy: 0.9980 - val_loss: 0.0105
Epoch 16/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.9910 - loss: 0.0251 - val_accuracy: 0.9910 - val_loss: 0.0288
Epoch 17/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.9695 - loss: 0.1368 - val_accuracy: 0.9880 - val_loss: 0.2077
Epoch 18/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.9950 - loss: 0.1453 - val_accuracy: 0.9960 - val_loss: 0.0912
Epoch 19/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 7ms/step - accuracy: 0.9936 - loss: 0.0688 - val_accuracy: 0.9980 - val_loss: 0.0517
Epoch 20/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.9967 - loss: 0.0440 - val_accuracy: 0.9960 - val_loss: 0.0217
Epoch 21/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.9954 - loss: 0.0211 - val_accuracy: 0.9980 - val_loss: 0.0144
Epoch 22/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.9973 - loss: 0.0183 - val_accuracy: 0.9960 - val_loss: 0.0131
Epoch 23/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.9885 - loss: 0.0338 - val_accuracy: 0.9980 - val_loss: 0.0103
Epoch 24/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.9943 - loss: 0.0173 - val_accuracy: 0.9860 - val_loss: 0.0498
Epoch 25/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.9780 - loss: 0.0559 - val_accuracy: 0.9920 - val_loss: 0.0296
Epoch 26/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 9ms/step - accuracy: 0.9950 - loss: 0.0185 - val_accuracy: 0.9980 - val_loss: 0.0091
Epoch 27/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 8ms/step - accuracy: 0.9944 - loss: 0.0212 - val_accuracy: 0.9980 - val_loss: 0.0085
Epoch 28/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 7ms/step - accuracy: 0.9944 - loss: 0.0154 - val_accuracy: 0.9920 - val_loss: 0.0240
Epoch 29/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.9736 - loss: 0.0827 - val_accuracy: 0.9930 - val_loss: 0.0259
Epoch 30/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.9977 - loss: 0.0199 - val_accuracy: 0.9980 - val_loss: 0.0134
Epoch 31/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.9979 - loss: 0.0149 - val_accuracy: 0.9980 - val_loss: 0.0116
Epoch 32/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.9875 - loss: 0.0374 - val_accuracy: 0.9980 - val_loss: 0.0103
Epoch 33/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.9944 - loss: 0.0167 - val_accuracy: 0.9970 - val_loss: 0.0102
Epoch 34/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.9958 - loss: 0.0131 - val_accuracy: 0.9930 - val_loss: 0.0251
Epoch 35/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.9950 - loss: 0.0154 - val_accuracy: 0.9970 - val_loss: 0.0086
Epoch 36/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.9880 - loss: 0.0309 - val_accuracy: 0.9950 - val_loss: 0.0179
Epoch 37/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 7ms/step - accuracy: 0.9971 - loss: 0.0144 - val_accuracy: 0.9970 - val_loss: 0.0095
Epoch 38/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.9982 - loss: 0.0089 - val_accuracy: 0.9420 - val_loss: 0.1502
Epoch 39/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.9591 - loss: 0.1021 - val_accuracy: 0.9980 - val_loss: 0.0100
Epoch 40/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.9923 - loss: 0.0255 - val_accuracy: 0.9950 - val_loss: 0.0154
Epoch 41/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 8ms/step - accuracy: 0.9956 - loss: 0.0144 - val_accuracy: 0.9980 - val_loss: 0.0087
Epoch 42/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 8ms/step - accuracy: 0.9939 - loss: 0.0198 - val_accuracy: 0.9950 - val_loss: 0.0146
Epoch 43/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 8ms/step - accuracy: 0.9954 - loss: 0.0162 - val_accuracy: 0.9970 - val_loss: 0.0086
Epoch 44/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.9940 - loss: 0.0215 - val_accuracy: 0.9830 - val_loss: 0.0494
Epoch 45/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.9785 - loss: 0.0576 - val_accuracy: 0.9770 - val_loss: 0.0658
Epoch 46/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.9870 - loss: 0.0255 - val_accuracy: 0.9980 - val_loss: 0.0077
Epoch 47/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.9959 - loss: 0.0132 - val_accuracy: 0.9960 - val_loss: 0.0086
Epoch 48/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.9904 - loss: 0.0319 - val_accuracy: 0.9960 - val_loss: 0.0174
Epoch 49/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.9979 - loss: 0.0091 - val_accuracy: 0.9980 - val_loss: 0.0081
Epoch 50/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.9971 - loss: 0.0101 - val_accuracy: 0.9860 - val_loss: 0.0429
Similarly, train another model with lr=0.0001 and store the output in history_2 variable.
Python
# get model
model_2 = get_model(lr=0.0001)
# train
history_2 = model_2.fit(x_d, y_d,
epochs = 50,
batch_size = 32,
validation_split=0.2
)
Total params: 76,545 (299.00 KB)
Trainable params: 76,545 (299.00 KB)
Non-trainable params: 0 (0.00 B)
None
Epoch 1/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 3s 10ms/step - accuracy: 0.5969 - loss: 0.6554 - val_accuracy: 0.5700 - val_loss: 0.6654
Epoch 2/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.6070 - loss: 0.6393 - val_accuracy: 0.5700 - val_loss: 0.6549
Epoch 3/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.5949 - loss: 0.6382 - val_accuracy: 0.5700 - val_loss: 0.6443
Epoch 4/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.6105 - loss: 0.6270 - val_accuracy: 0.5760 - val_loss: 0.6307
Epoch 5/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.6114 - loss: 0.6149 - val_accuracy: 0.5730 - val_loss: 0.6253
Epoch 6/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.6158 - loss: 0.6016 - val_accuracy: 0.5740 - val_loss: 0.6188
Epoch 7/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.6308 - loss: 0.5877 - val_accuracy: 0.5880 - val_loss: 0.5959
Epoch 8/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.6692 - loss: 0.5740 - val_accuracy: 0.6260 - val_loss: 0.5766
Epoch 9/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.6771 - loss: 0.5515 - val_accuracy: 0.7290 - val_loss: 0.5552
Epoch 10/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 7ms/step - accuracy: 0.7167 - loss: 0.5406 - val_accuracy: 0.6320 - val_loss: 0.5466
Epoch 11/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.7258 - loss: 0.5160 - val_accuracy: 0.8770 - val_loss: 0.5145
Epoch 12/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.7962 - loss: 0.4961 - val_accuracy: 0.8020 - val_loss: 0.4831
Epoch 13/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.8226 - loss: 0.4624 - val_accuracy: 0.7940 - val_loss: 0.4571
Epoch 14/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.8535 - loss: 0.4361 - val_accuracy: 0.8270 - val_loss: 0.4272
Epoch 15/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.8868 - loss: 0.3998 - val_accuracy: 0.8380 - val_loss: 0.3972
Epoch 16/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 8ms/step - accuracy: 0.9125 - loss: 0.3623 - val_accuracy: 0.9750 - val_loss: 0.3563
Epoch 17/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 7ms/step - accuracy: 0.9449 - loss: 0.3298 - val_accuracy: 0.9780 - val_loss: 0.3188
Epoch 18/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.9551 - loss: 0.2978 - val_accuracy: 0.9730 - val_loss: 0.2870
Epoch 19/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.9634 - loss: 0.2744 - val_accuracy: 0.9420 - val_loss: 0.2715
Epoch 20/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.9659 - loss: 0.2497 - val_accuracy: 0.9850 - val_loss: 0.2335
Epoch 21/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.9793 - loss: 0.2186 - val_accuracy: 0.9890 - val_loss: 0.2077
Epoch 22/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.9891 - loss: 0.1992 - val_accuracy: 0.9860 - val_loss: 0.1919
Epoch 23/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.9916 - loss: 0.1724 - val_accuracy: 0.9940 - val_loss: 0.1666
Epoch 24/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.9911 - loss: 0.1564 - val_accuracy: 0.9920 - val_loss: 0.1512
Epoch 25/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.9934 - loss: 0.1404 - val_accuracy: 0.9730 - val_loss: 0.1680
Epoch 26/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.9912 - loss: 0.1351 - val_accuracy: 0.9840 - val_loss: 0.1434
Epoch 27/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.9947 - loss: 0.1145 - val_accuracy: 0.9940 - val_loss: 0.1115
Epoch 28/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.9925 - loss: 0.1081 - val_accuracy: 0.9940 - val_loss: 0.1015
Epoch 29/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.9919 - loss: 0.1013 - val_accuracy: 0.9940 - val_loss: 0.0933
Epoch 30/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.9970 - loss: 0.0869 - val_accuracy: 0.9910 - val_loss: 0.1032
Epoch 31/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.9959 - loss: 0.0809 - val_accuracy: 0.9950 - val_loss: 0.0807
Epoch 32/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 7ms/step - accuracy: 0.9949 - loss: 0.0772 - val_accuracy: 0.9910 - val_loss: 0.0796
Epoch 33/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 8ms/step - accuracy: 0.9974 - loss: 0.0693 - val_accuracy: 0.9940 - val_loss: 0.0714
Epoch 34/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 8ms/step - accuracy: 0.9960 - loss: 0.0641 - val_accuracy: 0.9950 - val_loss: 0.0660
Epoch 35/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.9962 - loss: 0.0560 - val_accuracy: 0.9890 - val_loss: 0.0830
Epoch 36/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.9968 - loss: 0.0601 - val_accuracy: 0.9910 - val_loss: 0.0606
Epoch 37/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.9978 - loss: 0.0519 - val_accuracy: 0.9950 - val_loss: 0.0507
Epoch 38/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.9951 - loss: 0.0482 - val_accuracy: 0.9950 - val_loss: 0.0505
Epoch 39/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.9969 - loss: 0.0454 - val_accuracy: 0.9950 - val_loss: 0.0446
Epoch 40/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.9981 - loss: 0.0411 - val_accuracy: 0.9950 - val_loss: 0.0424
Epoch 41/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.9969 - loss: 0.0406 - val_accuracy: 0.9950 - val_loss: 0.0397
Epoch 42/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.9970 - loss: 0.0380 - val_accuracy: 0.9930 - val_loss: 0.0418
Epoch 43/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.9966 - loss: 0.0399 - val_accuracy: 0.9950 - val_loss: 0.0359
Epoch 44/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.9961 - loss: 0.0364 - val_accuracy: 0.9950 - val_loss: 0.0341
Epoch 45/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.9973 - loss: 0.0323 - val_accuracy: 0.9960 - val_loss: 0.0337
Epoch 46/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.9977 - loss: 0.0289 - val_accuracy: 0.9950 - val_loss: 0.0328
Epoch 47/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.9975 - loss: 0.0307 - val_accuracy: 0.9940 - val_loss: 0.0419
Epoch 48/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 7ms/step - accuracy: 0.9977 - loss: 0.0283 - val_accuracy: 0.9960 - val_loss: 0.0297
Epoch 49/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 1s 9ms/step - accuracy: 0.9972 - loss: 0.0282 - val_accuracy: 0.9950 - val_loss: 0.0342
Epoch 50/50
125/125 ━━━━━━━━━━━━━━━━━━━━ 2s 12ms/step - accuracy: 0.9950 - loss: 0.0277 - val_accuracy: 0.9940 - val_loss: 0.0333As stated above, the history objects from both the training instances are stored in their respective outputs.
The epochwise values of the loss and metrics are stored in the history attribute of the outputs. It is a dictionary, with appropriate keys for loss and metrics.
In our case, the epochwise accuracy of the training and validation data are stored in keys accuracy and val_accuracy, respectively. Also, the loss values are stored in loss and val_loss keys.
Python
print(history_1.history.keys())dict_keys(['accuracy', 'loss', 'val_accuracy', 'val_loss'])When we plot how the loss and accuracy changes with each epoch in both models, which have different learning rates, we can extract some useful information about the training process.
Let’s plot them first.
Python
fig , ax = plt.subplots(2,2, figsize=(8,6), sharex=True)
# accuracy history_1
ax[0, 0].plot(history_1.history['accuracy'], label='accuracy')
ax[0, 0].plot(history_1.history['val_accuracy'], label='val_accuracy')
ax[0, 0].legend()
ax[0, 0].set_title('Accuracy (lr=1e-2)')
# accuracy history_2
ax[0, 1].plot(history_2.history['accuracy'], label='accuracy')
ax[0, 1].plot(history_2.history['val_accuracy'], label='val_accuracy')
ax[0, 1].legend()
ax[0, 1].set_title('Accuracy (lr=1e-4)')
# loss history_1
ax[1, 0].plot(history_1.history['loss'], label='loss')
ax[1, 0].plot(history_1.history['val_loss'], label='val_loss')
ax[1, 0].legend()
ax[1, 0].set_title('Loss (lr=1e-2)')
ax[1, 0].set_xlabel('epochs')
# loss history_2
ax[1, 1].plot(history_2.history['loss'], label='loss')
ax[1, 1].plot(history_2.history['val_loss'], label='val_loss')
ax[1, 1].legend()
ax[1, 1].set_title('Loss (lr=1e-2)')
ax[1, 1].set_xlabel('epochs')
plt.show()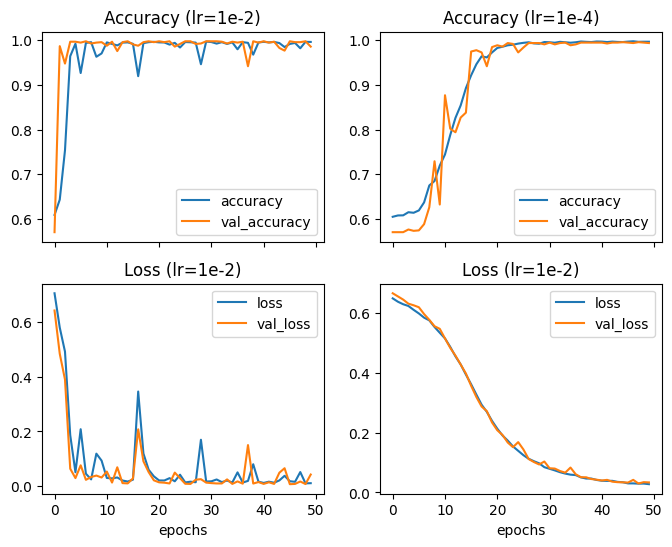
Interpretation of the results
We see that, at high learning rate, i.e. 0.01, The accuracy reaches close to 1, very quickly, even before 10 epochs. The accuracy of the model with low learning rate, i.e. 0.0001, reach to maximum in about 20 to 30 epochs.
Similarly, the loss also takes about 40 epochs to decrease to its minimum value in model with lower learning rate.
With high learning rate, even though the model reaches to its optimum quickly, the values of the loss and accuracy vary significantly with passing epochs. It means that they are deviating too much from the optimum value.
With lower learning rates, the optimum is reached slower but once it is attained, the metrics do not vary much. This gives us a model with stable weights which are closer to the optimum.
We can also see that with lower learning rate the accuracy values attain their maximum and remain almost constant after about 30 epochs. The loss values continue to decrease even after 30 epochs. Decreasing loss after attaining maximum metric scores may result in overfitting of the model. This would result in bad performance on test data later.
Therefore, from the plot, we can decide that 30 epochs are sufficient to get a well-trained model.
From the above example, we saw how the History object helped us visualize the epochwise changes in the metrics during trainig of a model. It also gave us some idea about how to select the learning rate of the optimizer.
Similarly, we can track other metrics such as precision and recall during the training and gain more insights about the training process, and select hyperparameters so that a better model is obtained after training.